3 načina za pronalaženje kvadratnih korijena bez kalkulatora

2024 Autor: Jason Gerald | [email protected]. Zadnja promjena: 2023-12-16 11:15

Kvadratni korijen broja lako je pronaći ako je odgovor cijeli broj. Ako odgovor nije cijeli broj, možete slijediti niz procesa da biste dobili kvadratni korijen, čak i ako ne koristite kalkulator. Za to morate razumjeti osnove množenja, zbrajanja i dijeljenja.

Korak

Metoda 1 od 3: Pronalaženje kvadratnog korijena cijelog broja

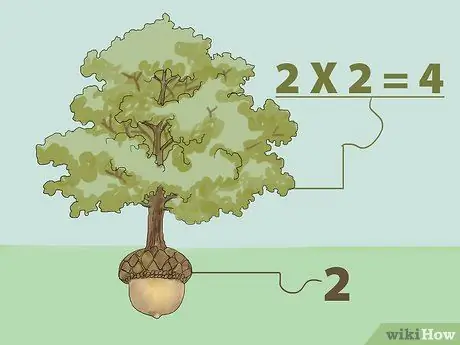
Korak 1. Množenjem pronađite savršeni kvadratni korijen

Kvadratni korijen broja je broj koji, pomnožen sam sa sobom, vraća izvorni broj. Drugim riječima: "Koji broj možemo sami pomnožiti da bismo dobili željeni broj?"

• Na primjer, kvadratni korijen iz 1 je 1 jer je 1 pomnoženo s 1 1 (1X1 = 1). Dakle, kvadratni korijen iz 4 je 2 jer je 2 pomnoženo s 2 4 (2X2 = 4). Zamislite koncept kvadratnog korijena kao stablo. Drvo raste iz sjemena. Dakle, stablo je veće od sjemena, koje raste iz sjemena koje mu je korijen. Iz gornjeg primjera 4 je stablo, a 2 je sjeme.
• Dakle, kvadratni korijen iz 9 je 3 (3X3 = 9), od 16 je 4 (4X4 = 16), od 25 je 5 (5X5 = 25), od 36 je 6 (6X6 = 36), od 49 je 7 (7X7 = 49), od 64 je 8 (8X8 = 64), od 81 je 9 (9X9 = 81), a od 100 je 10 (10X10 = 100).

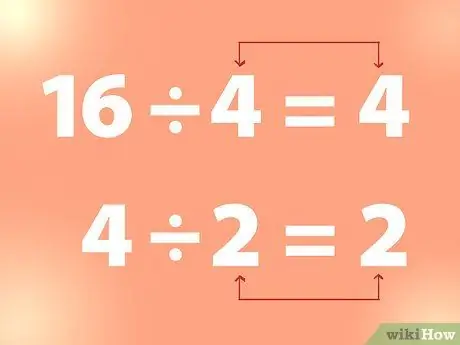
Korak 2. Pomoću kontinuiranog dijeljenja pronađite kvadratni korijen

Da biste pronašli kvadratni korijen cijelog broja, cijeli broj možete dijeliti s brojem dok ne dobijete broj koji je jednak djelitelju.

• Primjer: 16 podijeljeno s 4 je 4. I 4 podijeljeno s 2 je 2, i tako dalje. Dakle, iz gornjeg primjera 4 je kvadratni korijen iz 16, a 2 kvadratni korijen iz 4.
• Savršeni četvrtasti korijeni nemaju razlomaka ili decimala jer su cijeli brojevi.

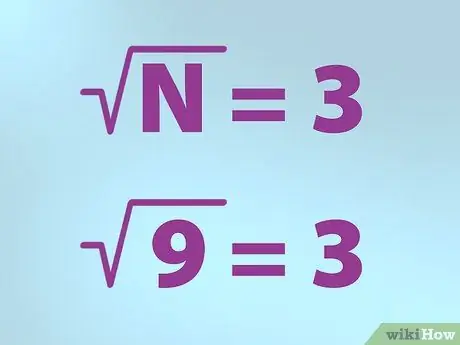
Korak 3. Upotrijebite ispravan simbol za kvadratni korijen

Matematičari koriste poseban simbol za predstavljanje kvadratnog korijena. Oblik je poput kvačice s plusom u gornjem desnom kutu.

• N je jednak broju za koji želite pronaći kvadratni korijen. N se stavlja ispod kvačice.
• Dakle, ako želite pronaći kvadratni korijen od 9, napišite formulu stavljajući "N" (9) unutar kvačice (simbol "korijen"), zatim upišite znak jednakosti i nakon toga 3. To znači "kvadratni korijen iz 9 je jednako 3 ".

Metoda 2 od 3: Pronalaženje kvadratnog korijena drugog broja

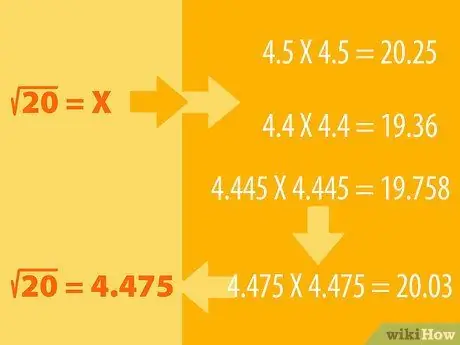
Korak 1. Pogodite i učinite proces eliminacije

Teško je pronaći kvadratni korijen necjelobrojnog broja. Međutim, to ne znači da je nemoguće.

• Na primjer, recimo da želite pronaći kvadratni korijen od 20. Znamo da je 16 savršen kvadrat čiji je kvadratni korijen 4 (4X4 = 16). Tada je 25 kvadratnih korijena 5 (5X5 = 25), pa kvadratni korijen od 20 mora ležati između dva.
• Možete pretpostaviti da je kvadratni korijen od 20. Sada je kvadrat 4.5 da biste vidjeli rezultat. Odnosno, sami pomnožimo 4, 5: 4, 5X4, 5. Provjerite je li odgovor veći ili manji od 20. Ako ste nagađali predaleko, pokušajte s drugim brojem (npr. 4, 6 ili 4, 4) i prilagodite pogodite prema tome. vi dok ne dobijete broj 20.
• Na primjer, 4, 5X4, 5 = 20, 25, pa logično moramo pronaći manji broj, možda 4, 4. 4, 4X4, 4 = 19, 36. Dakle, kvadratni korijen iz 20 mora ležati između 4, 5 i 4, 4. Pokušajte s 4, 445X4, 445. Rezultat je 19, 758. Rezultat je sve bliži. Pokušajte s drugim brojevima sve dok ne dobijete 4, 475X4, 475 = 20, 03. Zaokruženo, taj je broj jednak 20.

Korak 2. Upotrijebite postupak prosjeka

Ovaj proces također započinje pronalaženjem dva najbliža savršena kvadrata koji su okruženi brojem.

• Zatim taj broj podijelite s jednim od savršenih kvadratnih korijena. Uzmite odgovor, zatim pronađite prosjek između tog broja i broja za koji želite pronaći korijen (prosjek možete pronaći zbrajanjem dvaju i dijeljenjem s dva). Zatim početni broj podijelite s dobivenim prosjekom. Posljednji korak, pronađite prosjek rezultata s prosjekom izračunatim po prvi put.
• Zvuči komplicirano? Bilo bi lakše kad bi se dao primjer. Na primjer, 10 leži između dva savršena kvadrata 9 (3X3 = 9) i 16 (4X4 = 16). Kvadratni korijeni oba broja su 3 i 4. Dakle, podijelite 10 s prvim brojem, 3. Rezultat je 3, 33. Sada pronađite prosjek 3 i 3, 33 zbrajajući ih i dijeleći s 2. Rezultat je 3, 1667 Sada podijelite 10 sa 3.1667. Rezultat je 3.1579. Zatim pronađite prosjek 3.1579 i 3.1667 zbrajajući ih i dijeleći s 2. Rezultat je 3.1623.
• Provjerite svoj rezultat tako što ćete odgovor (u ovom primjeru 3, 1623) pomnožiti sam sa sobom. Rezultat 3,1623 pomnožen s 3,1623 ispada 10,001.

Metoda 3 od 3: Kvadriranje negativnih brojeva

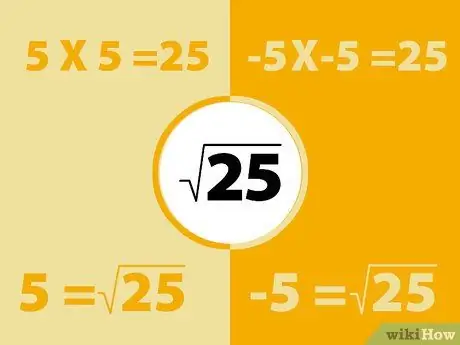
Korak 1. Kvadrirajte negativne brojeve istom metodom

Upamtite da je negativno vrijeme negativno pozitivno. Dakle, kvadrat negativnog broja će proizvesti pozitivan broj.

• Na primjer, -5X -5 = 25. Međutim, također zapamtite da je 5x5 = 25. Dakle, kvadratni korijen od 25 može biti -5 ili 5. U osnovi svaki broj ima dva kvadratna korijena.
• Slično, 3X3 = 9 i -3X -3 = 9, pa su kvadratni korijeni 9 3 i -3. Pozitivan kvadratni korijen naziva se "glavni korijen". U ovom trenutku samo trebamo obratiti pažnju na ovaj odgovor.

Korak 2. Upotrijebite kalkulator

Iako je najbolje moći ručno izračunati matematiku, postoji mnogo online kalkulatora za izračunavanje kvadratnih korijena.

• Potražite gumb kvadratnog korijena na običnom kalkulatoru.
• U mrežni kalkulator izravno unesite broj za koji želite pronaći vrijednost kvadratnog korijena i kliknite gumb. Računalo će vam pokazati vrijednost kvadratnog korijena.

Savjeti

• Uvijek imajte na umu nekoliko važnih savršenih kvadrata:

  • 0² = 0, 1² = 1, 3² = 9, 4² = 16, 5² = 25, 6² = 36, 7² = 49, 8² = 64, 9² = 81, 10² = 100,
  • Upamtite i ovaj savršeni kvadrat: 11² = 121, 12² = 144, 13² 169, 14² = 196, 15² = 225, 16² = 256, 17² = 289…
  • Imajte na umu i ovo: 10² = 100, 20² = 400, 30² = 900, 40² = 1600, 50² = 2500, …