Recipročno ili recipročno vrlo je korisno u svim vrstama algebarskih jednadžbi. Na primjer, kada jedan razlomak podijelite s drugim, prvi razlomak pomnožite s recipročnošću drugog. Također morate koristiti inverziju kada tražite jednadžbu prave.
Korak
Metoda 1 od 3: Pronalaženje inverza razlomka ili cijelog broja
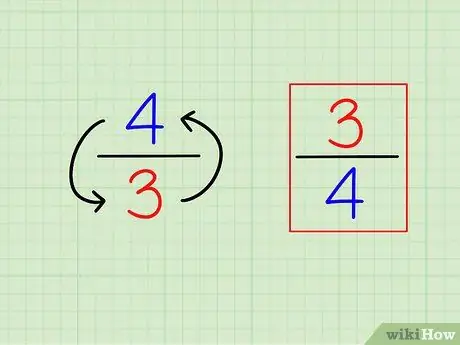
Korak 1. Pronađite recipročnu vrijednost razlomka obrnuvši je
Definicija „recipročno“ili suprotno vrlo je jednostavna. Da biste pronašli recipročnu vrijednost bilo kojeg cijelog broja, jednostavno izračunajte "1 (taj broj)". Za razlomke, recipročni je drugačiji razlomak, odnosno brojevi su "obrnuti" (inverzni).
- Na primjer, suprotno od 3/4 je 4/3.
- Bilo koji broj pomnožen s recipročnim povratkom 1.
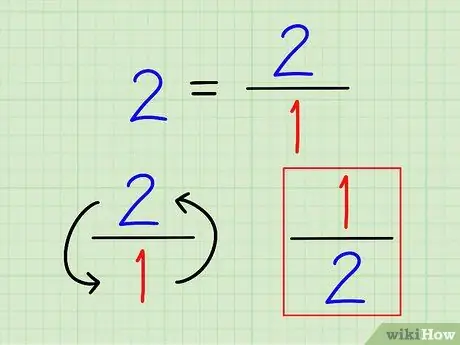
Korak 2. Napišite recipročnu vrijednost cijelog broja kao razlomak
Opet, recipročna vrijednost broja uvijek je 1 (taj broj). Za cijele brojeve napišite ih kao razlomke. Nema smisla izračunavati taj broj na decimalu.
Na primjer, recipročna vrijednost 2 je 1 2 = 1/2.
Metoda 2 od 3: Pronalaženje inversa mješovitog razlomka
Korak 1. Identificirajte mješovite brojeve
Mješoviti razlomci sastoje se od cijelih brojeva i razlomaka, poput 24/5. Postoje dva koraka za pronalaženje recipročnosti mješovitog broja kako je dolje opisano.
Korak 2. Pretvorite mješovite brojeve u nepravilne razlomke
Upamtite da 1 uvijek može biti napisano kao (broj)/(isti broj), a razlomci s istim nazivnikom (donji broj) mogu se zbrajati. Evo primjera pomoću 24/5:
- 24/5
- = 1 + 1 + 4/5
- = 5/5 + 5/5 + 4/5
- = (5+5+4)/5
- = 14/5.
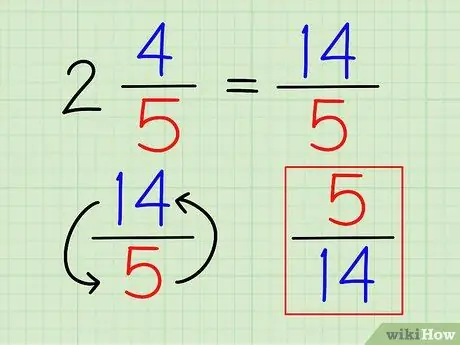
Korak 3. Preokrenite razlomak
Nakon što je broj potpuno napisan kao razlomak, možete pronaći njegovu recipročnu vrijednost kao i svaki drugi razlomak, obrnuvši razlomak.
U gornjem primjeru, recipročna vrijednost 14/5 je 5/14.
Metoda 3 od 3: Pronalaženje suprotnosti decimalnog mjesta
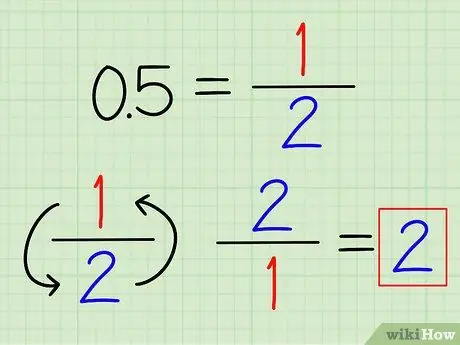
Korak 1. Pretvorite decimale u razlomke ako je moguće
Možda ćete prepoznati neke često korištene decimalne brojeve koji se lako mogu pretvoriti u razlomke. Na primjer, 0,5 = 1/2 i 0,25 = 1/4. Nakon što se decimalni broj pretvori u razlomak, jednostavno preokrenite razlomak kako biste pronašli njegovu recipročnu vrijednost.
Na primjer, recipročna vrijednost 0,5 je 2/1 = 2.
Korak 2. Napišite problem podjele
Ako ga ne možete pretvoriti u razlomak, izračunajte recipročnu vrijednost broja u obliku problema s dijeljenjem: 1 (decimalni). Za rješavanje možete koristiti kalkulator ili prijeći na sljedeći korak za ručno rješavanje.
Na primjer, možete pronaći povratnu vrijednost od 0,4 izračunavanjem 1 0,4
Korak 3. Promijenite problem dijeljenja tako da koristite cijele brojeve
Prvi korak za dijeljenje decimala je pomicanje decimalnog zareza sve dok svi brojevi nisu cijeli brojevi. Sve dok pomičete decimalnu točku oba broja za isti broj koraka, dobit ćete pravi odgovor.
Na primjer, možete koristiti 1 0, 4 i prepisati ga kao 10 4. U ovom slučaju pomaknete sve decimalne mjesta za jedan korak udesno, na isti način na koji svaki broj pomnožite s deset
Korak 4. Riješite problem pomoću duge podjele
Za izračunavanje recipročne vrijednosti upotrijebite metodu duge podjele. Ako izbrojite 10 4, dobit ćete odgovor 2, 5 što je recipročno 0, 4.
Savjeti
- Negativni recipročni broj broja isti je kao i redovni recipročni, po tome što se množi s negativnim. Na primjer, negativna recipročna vrijednost 3/4 je -4/3.
- Recipročno ili recipročno često se naziva "inverzija množenja".
- Broj 1 je sam sebi suprotan jer je 1 1 = 1.
- Broj 0 nema recipročne vrijednosti jer 0 nije definiran.
